匈牙利解法 – 12Reads管理百科

匈牙利解法概述

匈牙利解法是求解指派问题的一种新颖而又简便的解法，它是美国数学家库恩(Kuhn)于1955年提出的．库恩引用了匈牙利数学家康尼格(Konig)一个关于矩阵中0元素的定理：系数矩阵中独立0元素的最多个数等于能覆盖所有0元素的最小直线数，这种解法称为匈牙利法．

指派问题的最优解有这样一个性质，若从系数矩阵的一行(列)各元素中分别减去该行(列)的最小元素，得到新矩阵，那么以新矩阵为系数矩阵求得的最优解和用原矩阵求得的最优解相同．利用这个性质，可使原系数矩阵变换为含有很多0元素的新矩阵，而最优解保持不变．

匈牙利解法的步骤

具体操作为第一步：使指派问题的系数矩阵经变换，在各行各列中都出现0元素．(1)从系数矩阵的每行元素减去该行的最小元素；(2)再从所得系数矩阵的每列元素中减去该列的最小元素．第二步：进行试指派．若此时得到的mPn，应回到第一步，重新对系数矩阵进行变换。但要把第一步的过程改为(1)从系数矩阵的每列元素减去该列的最小元素；(2)再从所得系数矩阵的每行元素中减去该行的最小元素．这样做就使得新矩阵的0元素比较多些．再进入第二步进行试指派就可以得到最优解．利用前面的性质可以证明这个最优解就是我们所要求的原问题的最优解，从而使得求解变得更为简捷。

匈牙利解法原理

其基本原理是：为了实现目标极小，在系数矩阵元素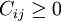 $C_{ij}\ge0$ 的条件下，如果能使矩阵具有一组处于不同行又不同列的零元素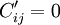（ $C^\prime_{ij}=0$ ）打上括号（），对应该元素的决策变量xij = 1，未打括号元素对应的决策变量Xij = 0，那么目标函数值 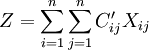$Z=\sum_{i=1}^n\sum_{j=1}^n C^\prime_{ij}X_{ij}$ 为最小，这样的组合解就是最优解。

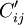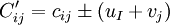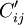定理1：从(cij)矩阵的每行(或列)减去或加上一个常数ui(或vj)构成新矩阵( $C^\prime_{ij}$ )， $C^\prime_{ij}=c_{ij}\pm(u_I+v_j)$ ，则对应( $C^\prime_{ij}$ )的(xij)最优解与原(cij)的最优解等价。

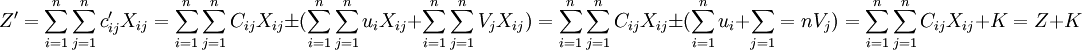
$Z^\prime=\sum_{i=1}^n\sum_{j=1}^n c_{ij}^\prime X_{ij}=\sum_{i=1}^n\sum_{j=1}^n C_{ij} X_{ij}\pm(\sum_{i=1}^n\sum_{j=1}^n u_i X_{ij}+\sum_{i=1}^n\sum_{j=1}^n V_j X_{ij})=\sum_{i=1}^n\sum_{j=1}^n C_{ij} X_{ij}\pm(\sum_{i=1}^n u_i+\sum_{j=1}=n V_j)=\sum_{i=1}^n\sum_{j=1}^n C_{ij} X_{ij}+K=Z+K$

证明：如从新矩阵中得到最优解(xij)，则其目标函数值达到极值：其中：K为一常数，故当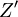 $Z^\prime$ 达到极值时Z也达到极值。所以(xij）也为原矩阵(cij)的最优解。

利用这个定理，可以使原系数矩阵(Cij)变换成含有很多0元素的新系数矩阵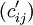 $(c^\prime_{ij})$ ，从而最优解保持不变。

独立的0元素：在系数矩阵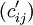 $(c^\prime_{ij})$ 中，位于不同行不同列的0元素。

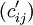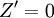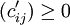若能在系数矩阵 $(c^\prime_{ij})$ 中找出n个独立的0元素,则令解矩阵(Xij)中对应这n个独立0元素的取值为1，其他元素取值为0。将其代入目标函数中得到 $Z^\prime=0$ ,因 $(c^\prime_{ij})\ge0$ ,故它一定是最小值。这就是以 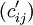$(c^\prime_{ij})$ 为系数矩阵的分派问题的最优解，也就是原问题的最优解。

非标准指派问题

匈牙利法只适用于符合以下三个条件的分派问题的求解：

① 目标函数为极小型；

② 系数矩阵为方阵；

③ 系数矩阵元素值非负。即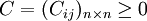： $C=(C_{ij})_{n\times n}\ge0$

对于不满足上述三个条件的分派问题应转化为标准指派问题。

1）当分派问题目标要求极大时，即求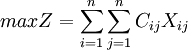 $max Z=\sum_{i=1}^n\sum^n_{j=1}C_{ij}X_{ij}$ ,此时，可把求极大型转变为求极小型，利用式：

max = Z = min( − Z)即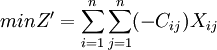： $min Z^\prime=\sum_{i=1}^n\sum^n_{j=1}(-C_{ij})X_{ij}$

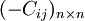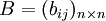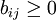再由定理1，矩阵 $(-C_{ij})_{n\times n}$ 每行均可加上一个常数M(或令Cij中最大元素为M即可)，令：bij = M − Cij，这时系数矩阵可变换为： $B=(b_{ij})_{n\times n}$ 这时， $b_{ij}\ge0$ ，B叫C的缩减矩阵。符合匈牙利法的条件。由定理1可知：所得的最小解就是原问题的最大解。

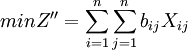
$min Z^{\prime\prime}=\sum_{i=1}^n\sum^n_{j=1}b_{ij}X_{ij}$

（2）系数矩阵不是方阵，目标仍为Min型问题：系数矩阵化为方阵。

其特点是：m个人分派做n项工作，系数矩阵(Cij)为m×n矩阵，m≠n。

①若 m < n ，则增添虚构的 s = n – m 行，补成方阵，但是对应的Cij = 0。

②若 m > n ，则增添虚构的 s = m – n 列，补成方阵，但是对应的Cij = 0。

匈牙利解法的示例

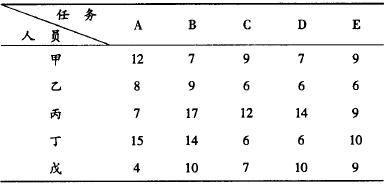
Image:匈牙利解法例题.jpg

步骤一：将这系数矩阵进行变换，使各行各列都出现0元素．从系数矩阵的每行元素减去该行的最小元素即得每行每列都有有0元素的系数矩阵．

$\begin{bmatrix}12 & 7 & 9 & 7 & 9 \\8 & 9 & 6 & 6 & 6 \\7 & 17 & 12 & 14 & 9 \\ 15 & 14 & 6 & 6 & 10 \\ 4 & 10 & 7 & 10 & 0 \end{bmatrix}$ $\to$ $\begin{bmatrix}5 & 0 & 2 & 0 & 2 \\2 & 3 & 0 & 0 & 0 \\0 & 10 & 5 & 7 & 2 \\ 9 & 8 & 0 & 0 & 4 \\ 0 & 6 & 3 & 6 & 5 \end{bmatrix}$

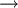
步骤二：进行试指派，找出独立的0元素．独立0元素用Θ表示，其它0用Φ表示得到

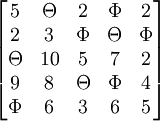$\begin{bmatrix}5 & \Theta & 2 & \Phi & 2 \\2 & 3 & \Phi & \Theta & \Phi \\ \Theta & 10 & 5 & 7 & 2 \\ 9 & 8 & \Theta & \Phi & 4 \\ \Phi & 6 & 3 & 6 & 5 \end{bmatrix}$ ……(1)

这里Θ的个数m=4,而n=5；问题没有得到求解，运用步骤三继续求解．

步骤三：作最少的直线覆盖所有的0元素，以确定该系数矩阵中能找到最多的独立元素数．为此按以下步骤进行．

(1)对没有Θ的行打√号：；

(2)对已打√号的行中所含0元素的列打√号；

(3)再对所有打√号的列中的含有@元素的行打√号；

(4)重复2、3直到得不出新的打√号的行列为止．

(5)对没有打√号的行画一横线，有打√号的列画一纵线，这就得到覆盖所有0元素的最少直线数．

令直线数为l．若l < n，说明必须再变换当前的系数矩阵，才能找到n个独立的0元素，为此转换步骤四；若l = n，而m < n，应回到步骤二，另行试探．

在此例中，对矩阵(1)按以下次序进行：

先在第五行旁打√，接着可判断应在第一列下打√，接着在第3行旁打√，经检查不能再打√了．对没有打√行画一直线以覆盖0元素，对打√的列画一直线以覆盖0元素，得：

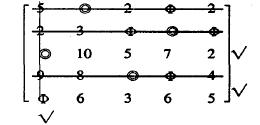Image:匈牙利解法步骤2.jpg ……(2)

由此可见l = 4 < n．所以应继续对(2)矩阵进行变换转步骤四．

步骤四：对(2)矩阵进行变换的目的是增加0元素．

为此在没有被直线覆盖的部分中找出最小元素．然后在打√行各元素中都减去这个最小元素，而在打√列的各元素上都加上这个最小元素，以保证原来0元素不变．这样得到新系数矩阵(它的最优解和原问题相同)．若得到n个独立的0元素，则已得最优解，否则回到步骤三重复进行．

在矩阵(2)中，在没有被覆盖部分(第3、5行)中找到最小元素为2，然后在第3、5行各元素分别减去2。给第l列各元素加2，得到新矩阵(3)

$\begin{bmatrix}7 & 0 & 2 & 0 & 2 \\4 & 3 & 0 & 0 & 0 \\ 0 & 8 & 3 & 5 & 0 \\ 11 & 8 & 0 & 0 & 4 \\ 0 & 4 & 1 & 4 & 3 \end{bmatrix}$ ……(3)

按步骤二，找出所有的独立0元素。得到矩阵(4)

$\begin{bmatrix}7 & \Theta & 2 & \Phi & 2 \\4 & 3 & \Phi & \Theta & \Phi \\ \Phi & 8 & 3 & 5 & \Theta \\ 11 & 8 & \Theta & \Phi & 4 \\ \Theta & 4 & 1 & 4 & 3 \end{bmatrix}$ ……(4)

它具有n个独立0元素．这就得到了最优解，相应解矩阵为

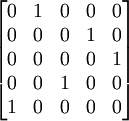
$\begin{bmatrix}0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \end{bmatrix}$

由解矩阵得最优指派方案：

甲——B，乙——D，丙——E，丁——C，戊——A

所需总时间为minz=32．